
Evidência Circular
O trabalho de Gerald Hawkins com os círculos ingleses começa através do livro Circular Evidence (Phanes Press, 1989) de Colin Andrews e Patrick Delgado, dois dos primeiros e então principais investigadores do tema. Hawkins realizou seus estudos em uma época em que os círculos ingleses ainda eram primariamente círculos e ingleses – hoje já incluem desenhos de rostos humanos e alienígenas, estando espalhados em diversas partes do mundo. [2]
O tema lhe chamou a atenção, e através do livro ele passou a analisar “estatisticamente” as medidas dos círculos, isto é, analisar razões e relações entre comprimentos, diâmetros, larguras ou áreas de certas partes de formações em cereais. Para sua surpresa, teria descoberto repetidas vezes entre tais medidas razões de números inteiros como 1, 9/8, 5/4, 4/3, 3/2... Podem parecer razões aleatórias, mas são nada menos que razões que constituem parte da escala diatônica justa. Esta é a escala por trás das notas musicais que conhecemos (Dó, Ré, Mi, Fá, Sol...), e segundo Hawkins indicava algo sobre a inteligência de seus autores. A chance de que tais razões surgissem fortuitamente, sempre segundo ele, era de 1 em 25.000. [3]

Como se não bastasse, tempos depois descobriu que alguns círculos seriam demonstrações geométricas de teoremas matemáticos. Teoremas são proposições a ser demonstradas, e o mais famoso deve ser o teorema de Pitágoras (“a soma dos quadrados dos catetos é igual ao quadrado de hipotenusa”). O teorema de Pitágoras é conhecido há milhares de anos e ensinado a praticamente toda pessoa alfabetizada, porém os teoremas indicados em alguns círculos seriam teoremas Euclidianos não tão conhecidos ao cidadão comum.
Tudo isso ainda culminaria quando Hawkins notou que os quatro teoremas indicados geometricamente nos círculos eram casos especiais de um quinto teorema geral, desconhecido até então. Em 1992 o problema foi exposto na revista Science News como um desafio aos 267.000 leitores, [4] mas ninguém deduziu o quinto teorema e sua demonstração.

Gerald Hawkins havia encontrado um “perfil intelectual” dos autores de círculos, e não parecia muito compatível com o de meros brincalhões como Douglas Bower e David Chorley, que pouco antes haviam sido anunciados como autores de boa parte dos círculos.
Hawkins escreveu a eles perguntando por que haviam se utilizado da escala diatônica, apenas para não receber resposta alguma. A pergunta que se faz é: se o “perfil intelectual” dos autores de círculos indicava um conhecimento da escala diatônica, teoremas euclidianos e indicações de teoremas desconhecidos, e não eram Doug e Dave, quem realmente estava por trás de tudo isto?

Aleatoriedade
O valor de 1/25.000 para a chance de que razões diatônicas surgissem aleatoriamente é impressionante. O certo é que os círculos ingleses não são tão aleatórios em seu desenho: na época em que o professor fez seu estudo, sempre envolviam círculos e semicírculos intercalados, geralmente em disposição de triângulos eqüiláteros e hexágonos, com alguma variação ocasional incluindo quadrados, pentágonos e outros polígonos regulares. O reaproveitamento de medidas como o raio do círculo principal é algo muito comum, o que gera justamente a profusão de triângulos eqüiláteros e hexágonos como base de desenhos, e há uma explicação muito simples para tal. É o reaproveitamento de uma corda usada para traçar o círculo principal. Dê um compasso para uma criança, e ela bem pode acabar reaproveitando uma mesma abertura diversas vezes, gerando desenhos muito similares.
Mais do que isso, é importante notar que Hawkins não encontrou apenas razões diatônicas. Segundo ele, encontrou repetidas vezes tais razões em 12 de 19 círculos com “medidas acuradas” do livro Circular Evidence. Mas mesmo entre estes 12 círculos com razões diatônicas, diversas proporções entre outras medidas equivaliam a razões não-diatônicas. Ou seja, o fato é que embora nem todos os círculos apresentassem razões diatônicas mesmo entre algumas de suas medidas, todos eles continham sim razões não-diatônicas!
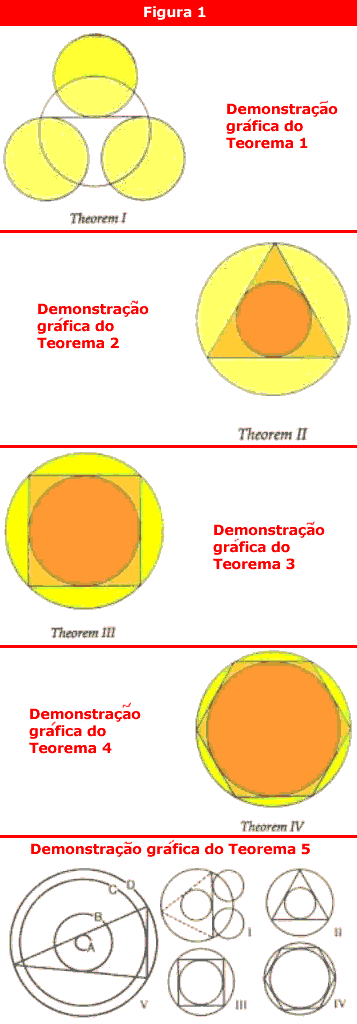
Demonstração de teoremas
Pode parecer uma questão de ponto de vista, e de certa forma é. Mas avaliá-los reforça a constatação evidente de que os círculos ingleses não são completamente aleatórios, e o encontro de razões diatônicas entre algumas de suas medidas, e não em outras, não deve ser extraordinário por si mesmo.
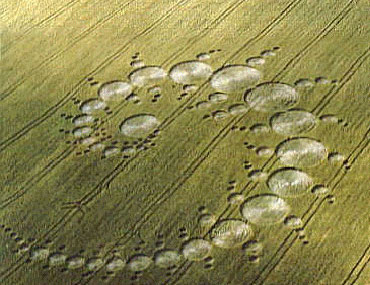
FOTOS DE CIRCULOS























Nenhum comentário:
Postar um comentário